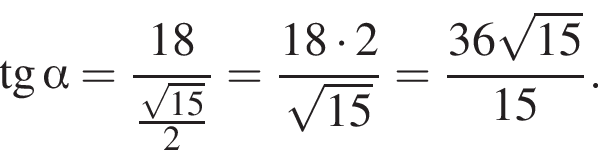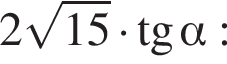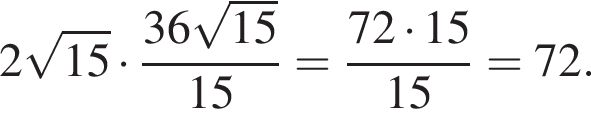Используя данные рисунка, найдите градусную меру угла 1 треугольника АВС.
Среди дробей ![]()
![]()
![]()
![]()
![]() укажите ту, которая равна дроби
укажите ту, которая равна дроби ![]()
Если MK — диаметр, O — центр окружности,
 (см. рис.), то градусная мера вписанного угла NMK равна:
(см. рис.), то градусная мера вписанного угла NMK равна:
На изготовление 25 письменных столов расходуется 3,4 м3 древесины. Сколько кубических метров древесины потребуется на изготовление 110 таких столов?
Вычислите 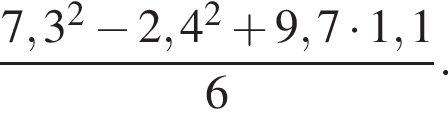
В магазин поступило 43 коробки с маслом по 110 пачек масла в каждой. Какое наименьшее количество пачек масла необходимо продавать ежедневно, чтобы масло было распродано не более чем за 60 дней?
На рисунке изображен график функции y = f(x), которая определена на промежутке [−6; 6]. Найдите количество целых значений x, при которых выполняется неравенство 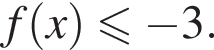 (Черными точками отмечены узлы сетки, через которые проходит график, функции y = f(x).
(Черными точками отмечены узлы сетки, через которые проходит график, функции y = f(x).
Результат упрощения выражения 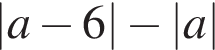 при
при 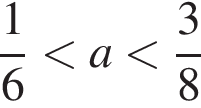 имеет вид:
имеет вид:
ABCDA1B1C1D1 — прямоугольный параллелепипед, у которого AB = 4, AD = 3,
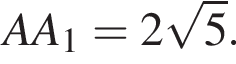 Найдите длину пространственной ломаной B1A1C1D (см. рис.).
Найдите длину пространственной ломаной B1A1C1D (см. рис.).
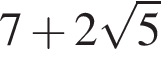
Укажите номера верных неравенств, если известно, что 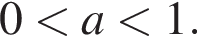
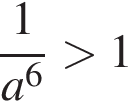
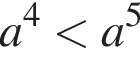

На координатной плоскости даны точки A(−5; 1) и D(−5; −4). Точка С симметрична точке А относительно оси ординат, а точка В симметрична точке D относительно начала координат. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Длина большей диагонали четырехугольника ABCD равна ...
Б) Длина наибольшей стороны четырехугольника ABCD равна ...
B) Площадь четырехугольника ABCD равна ...
1) 30
2) 50
3) ![]()
4) 40
5) ![]()
6) ![]()
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Найдите произведение большего корня на количество корней уравнения 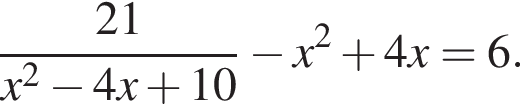
Найдите модуль разности наибольшего и наименьшего корней уравнения 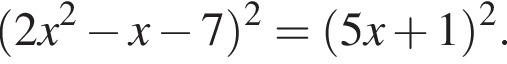
На пастбище квадратной формы загон для скота огорожен так, как показано на рисунке. Все размеры указаны в метрах. Найдите площадь загона (в м2), если площадь пастбища в 32 раза больше площади загона.
Найдите произведение наименьшего корня (в градусах) на количество различных корней уравнения  на промежутке (−90°; 90°).
на промежутке (−90°; 90°).
Найдите сумму целых решений неравенства 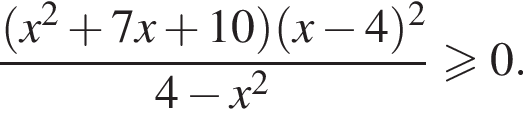
Четырёхугольник ABCD вписан в окружность. Если 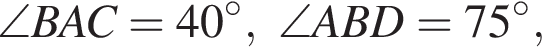 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите сумму корней уравнения
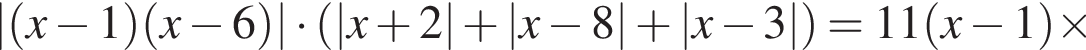
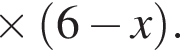
Найдите значение выражения 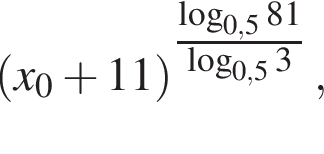 где x0 — корень уравнения
где x0 — корень уравнения 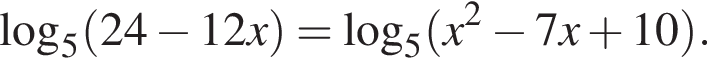
Найдите произведение наибольшего целого решения на количество целых решений неравенства 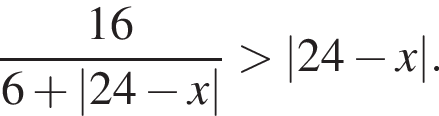
Из двух растворов с различным процентным содержанием спирта массой 100 г и 900 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Прямоугольный треугольник, длина гипотенузы которого равна 10, высота, проведенная к ней, равна 3, вращается вокруг прямой, перпендикулярной гипотенузе и проходящей в плоскости треугольника через вершину большего острого угла. Найдите объем V тела вращения и в ответ запишите значение выражения ![]()
Радиус основания цилиндра равен 13. Плоскость, параллельная оси цилиндра, пересекает цилиндр по прямоугольнику с площадью, равной 108. Найдите значение выражения ![]() где V — объем цилиндра, если расстояние от плоскости сечения до оси цилиндра равно
где V — объем цилиндра, если расстояние от плоскости сечения до оси цилиндра равно ![]()
Найдите произведение наименьшего целого решения на количество всех натуральных решений системы неравенств
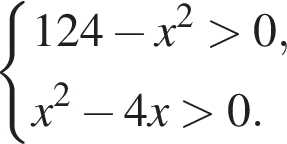
Найдите суму всех целых решений неравенства 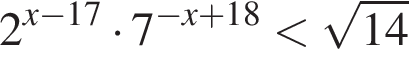 на промежутке (−25; 25).
на промежутке (−25; 25).
В большой круг шара вписан треугольник, длина одной из сторон которого равна 6, а противолежащий этой стороне угол равен 120°. Найдите значение выражения 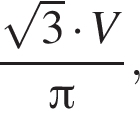 где V — объем шара.
где V — объем шара.
Найдите (в градусах) сумму различных корней уравнения 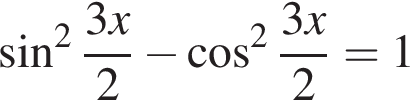 на промежутке
на промежутке 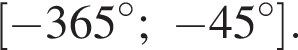
Найдите произведение наибольшего целого решения на количество всех натуральных решений неравенства 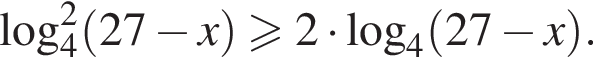
Два крана, работая одновременно, разгрузили баржу за 9 ч. Если бы половину баржи разгрузил первый кран, а затем оставшуюся часть — второй кран, то баржа была бы разгружена за 50 ч. За какое время (в часах) первый кран, работая один, разгрузил бы всю баржу, если известно, что он работает медленнее, чем второй кран?
Основанием четырехугольной пирамиды является ромб, у которого косинус угла равен ![]() и длина стороны равна 8. Все боковые грани пирамиды наклонены к плоскости ее основания под углом α, а высота пирамиды равна 18. Найдите значение выражения
и длина стороны равна 8. Все боковые грани пирамиды наклонены к плоскости ее основания под углом α, а высота пирамиды равна 18. Найдите значение выражения 

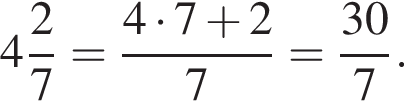
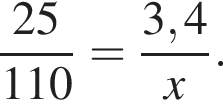 Тогда
Тогда 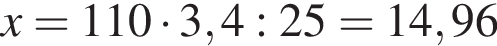 м3.
м3.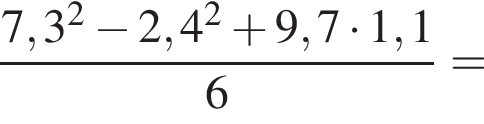
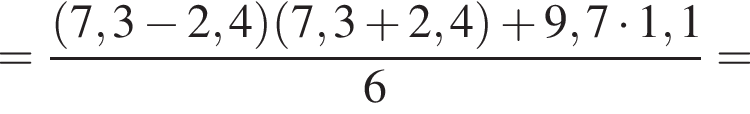
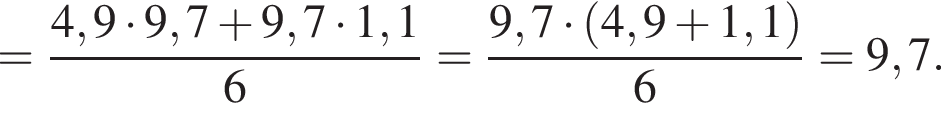
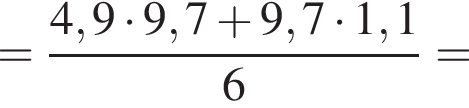
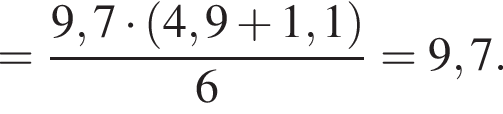
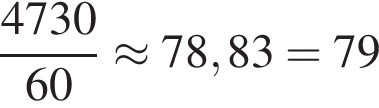 пачек масла.
пачек масла.
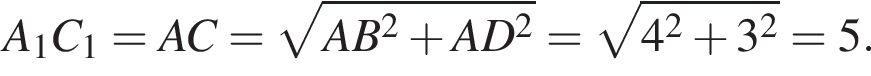
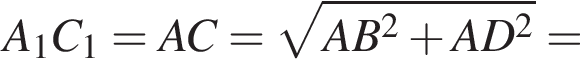
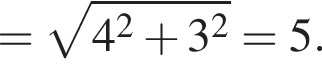
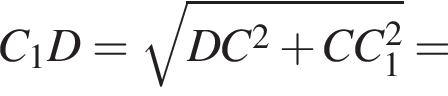
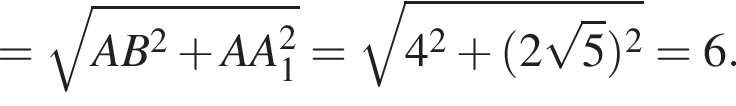
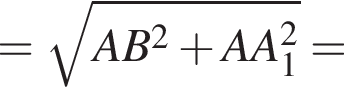
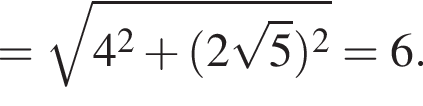
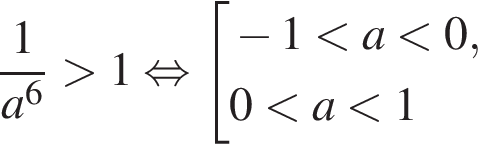 — неравенство верно;
— неравенство верно;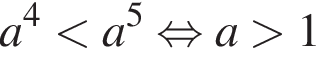 — неравенство неверно;
— неравенство неверно; — неравенство неверно;
— неравенство неверно;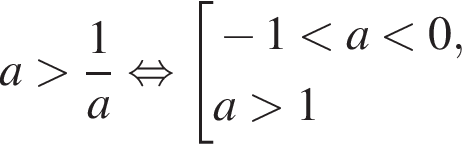 — неравенство неверно;
— неравенство неверно;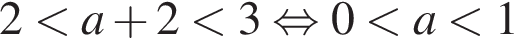 — неравенство верно.
— неравенство верно.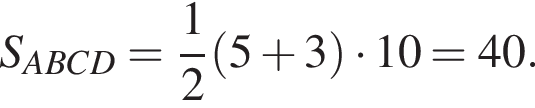
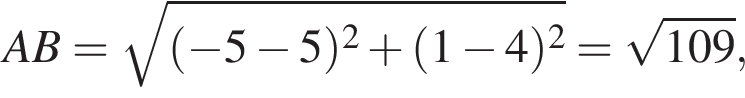
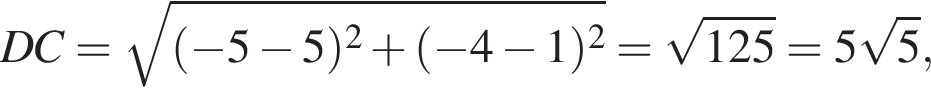
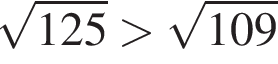 и тем более
и тем более 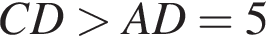 и
и 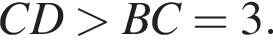 Значит, наибольшая боковая сторона имеет длину
Значит, наибольшая боковая сторона имеет длину 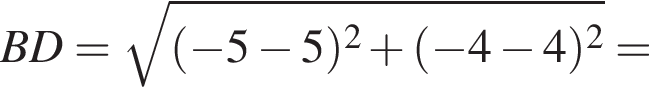
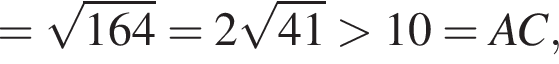
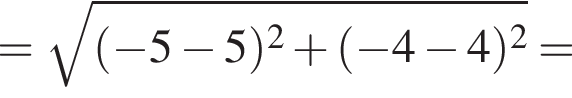
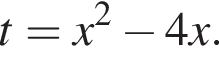 Тогда:
Тогда: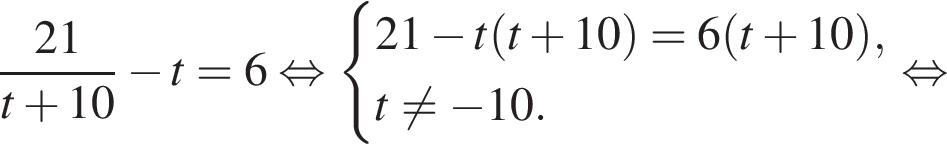
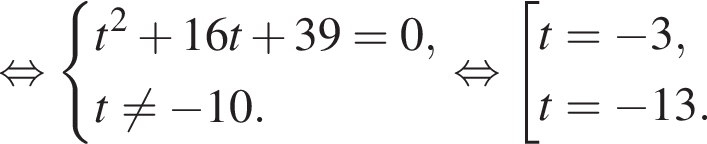
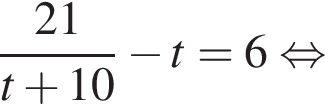
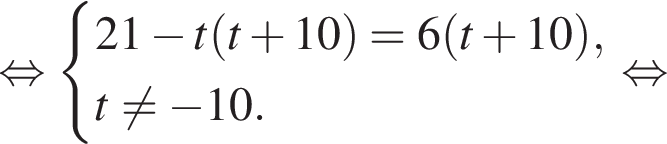
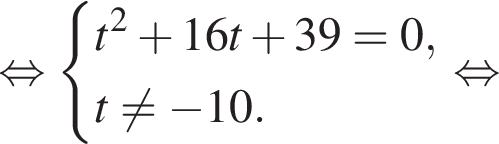
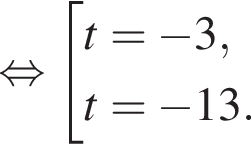
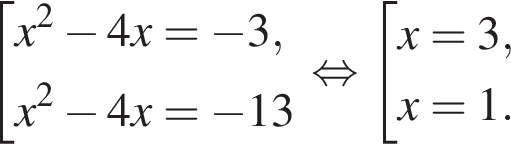
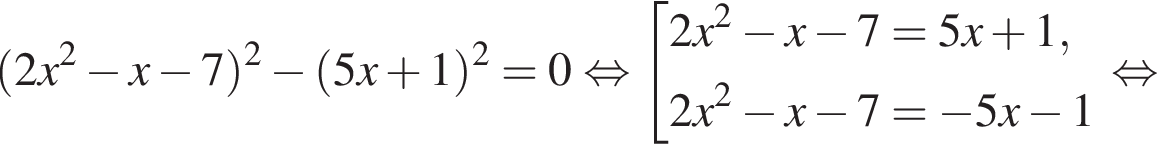
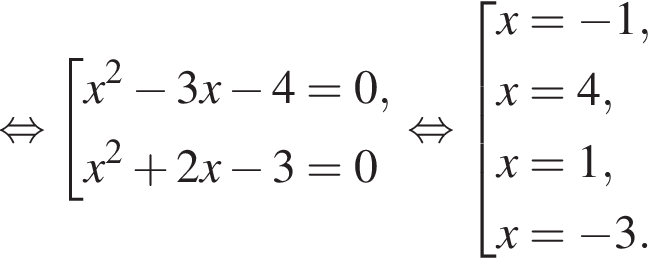
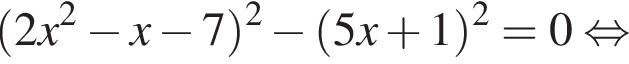
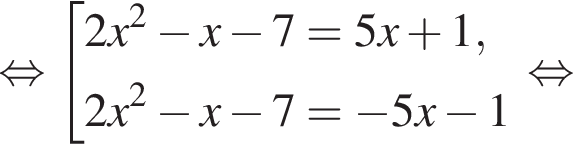
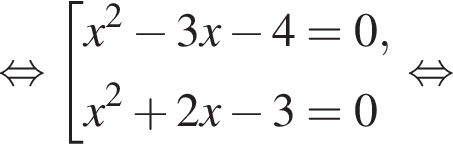
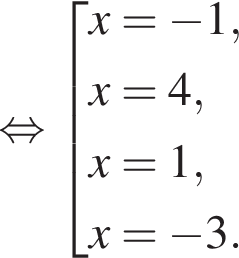
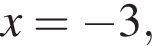 модуль разности наибольшего и наименьшего корней уравнения равен 7.
модуль разности наибольшего и наименьшего корней уравнения равен 7.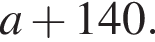 Откуда
Откуда 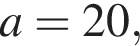 а площадь загона равна
а площадь загона равна 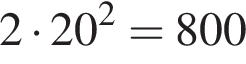 м2.
м2.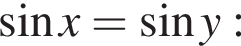
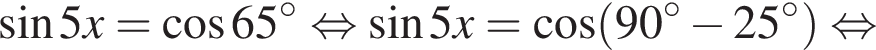
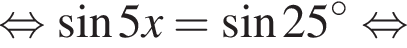
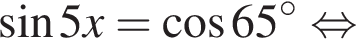

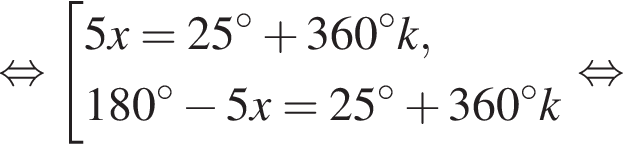
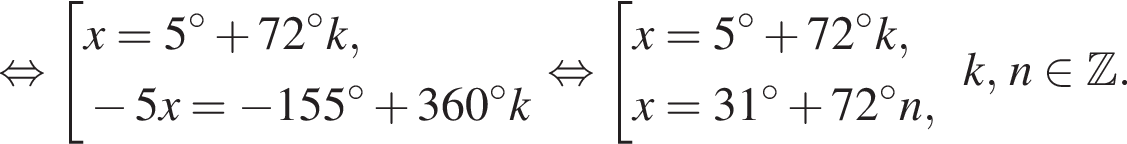
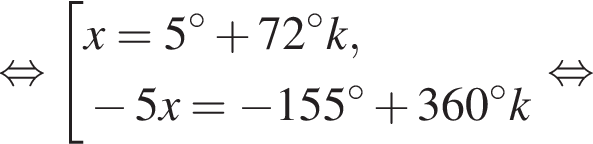
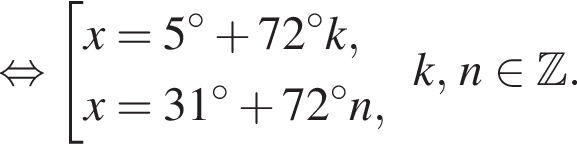

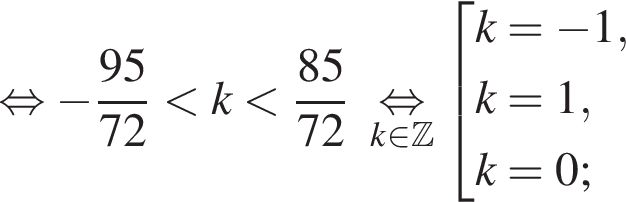


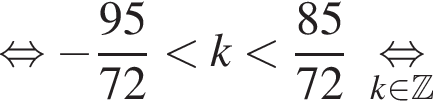
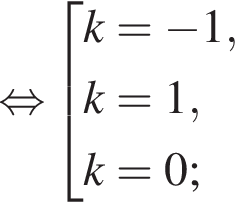

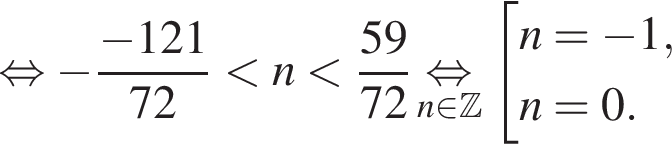
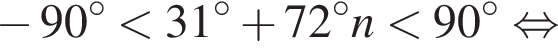

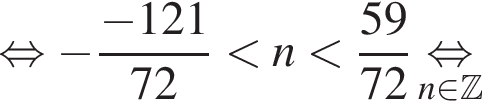
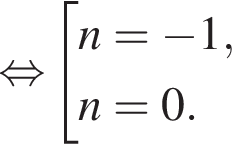
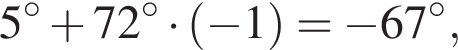
 и
и 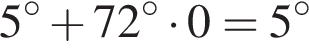 из первой серии и корни
из первой серии и корни  и
и 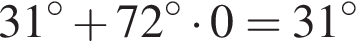 из второй. Наименьший из корней равен
из второй. Наименьший из корней равен 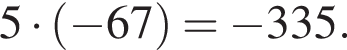
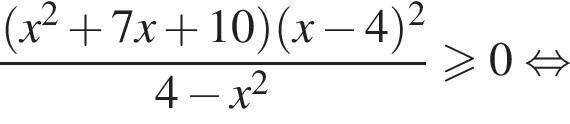
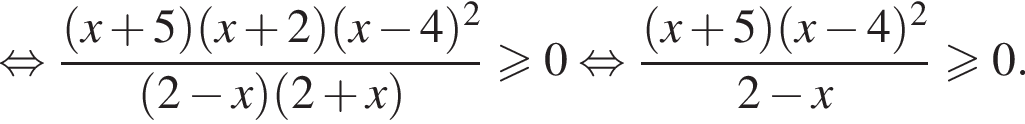
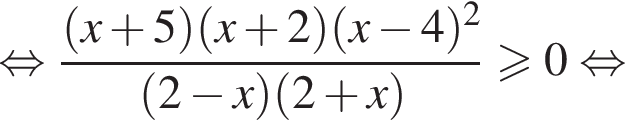
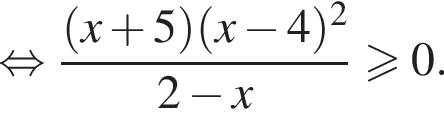
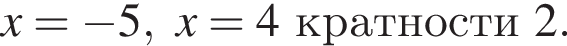 Корень знаменателя:
Корень знаменателя: 

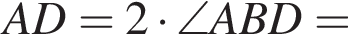

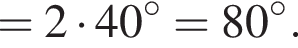
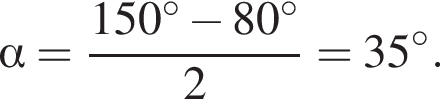

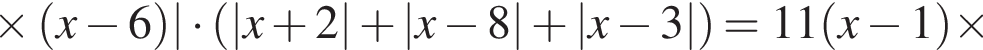
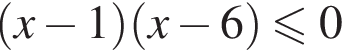 :
: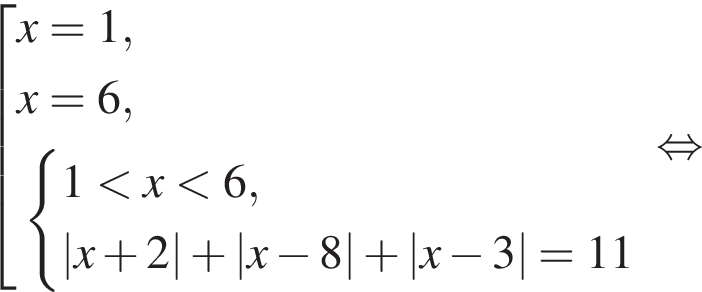
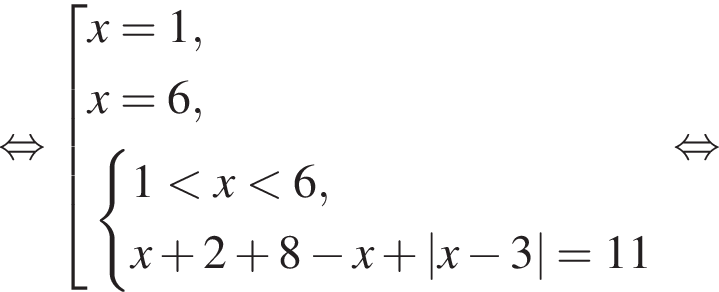
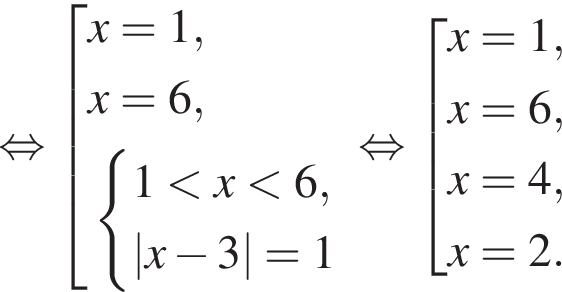
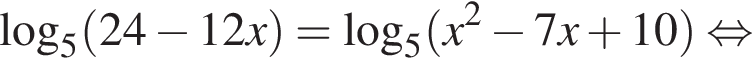
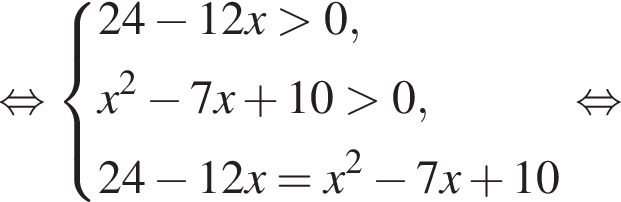
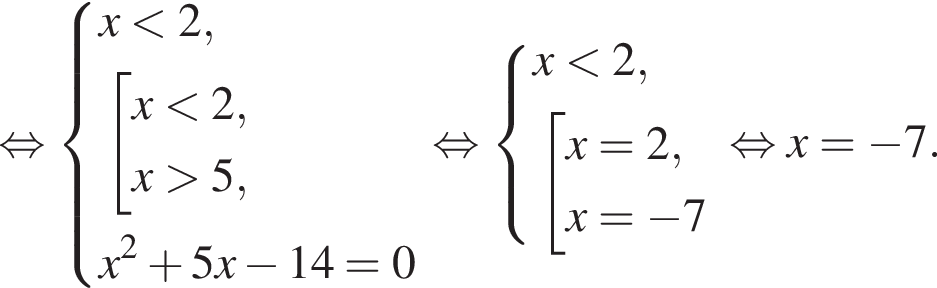
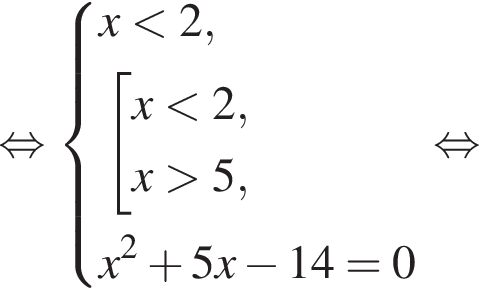
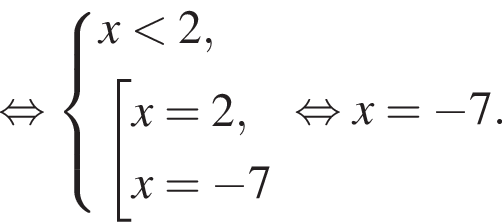
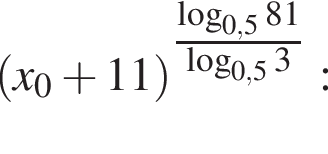
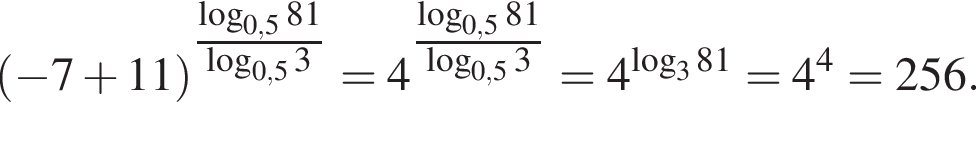
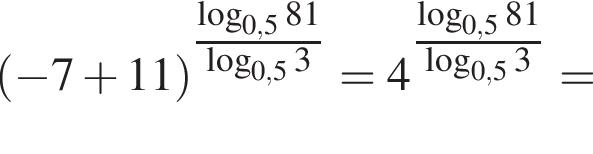

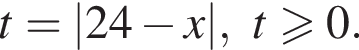 Имеем:
Имеем: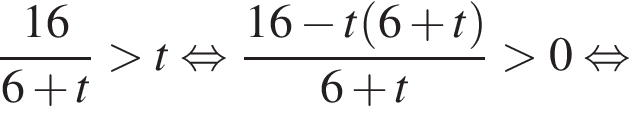
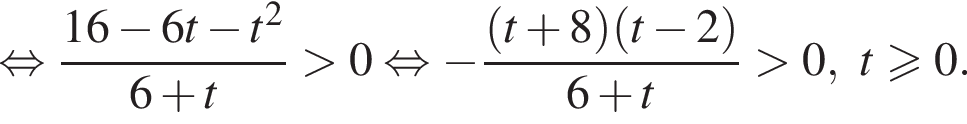
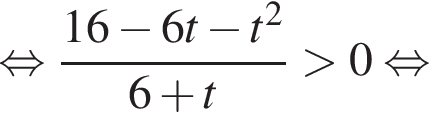
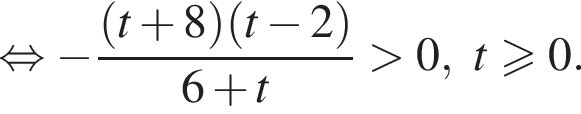
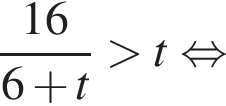
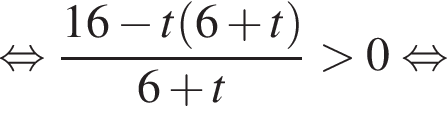
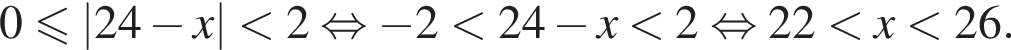
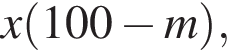 во втором —
во втором — 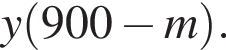 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 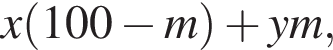 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда: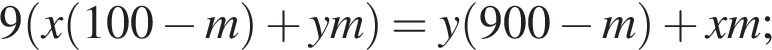
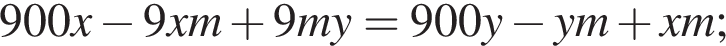

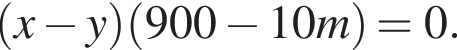

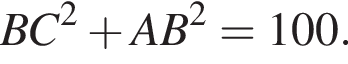 Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем:
Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем: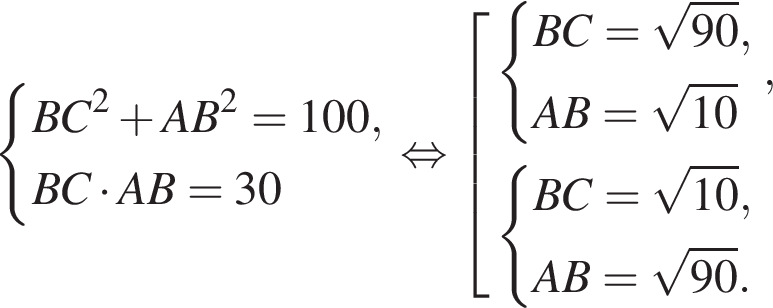
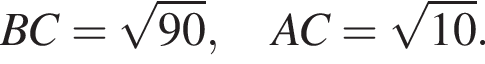 По теореме Пифагора найдем
По теореме Пифагора найдем 
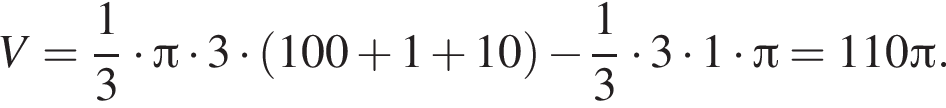
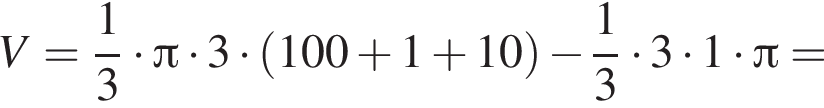
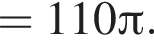
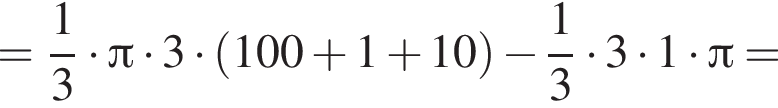
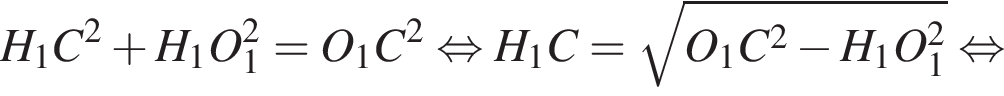
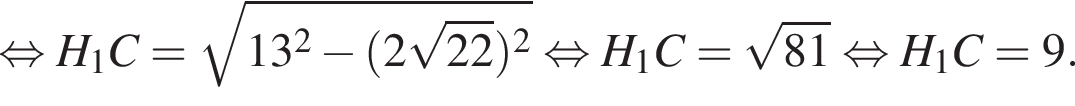
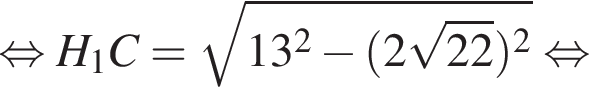
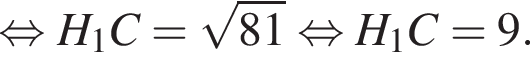
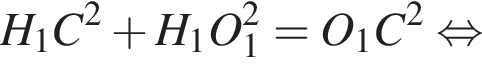
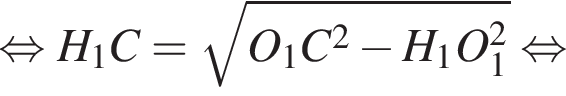
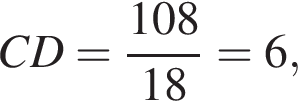 что равно высоте h цилиндра. Найдем объем цилиндра:
что равно высоте h цилиндра. Найдем объем цилиндра: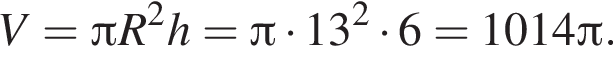
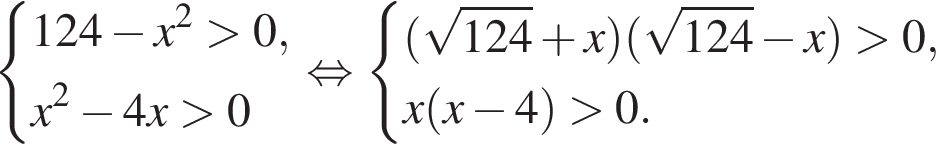
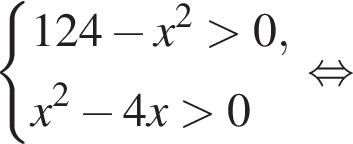
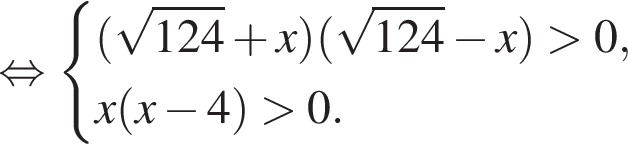
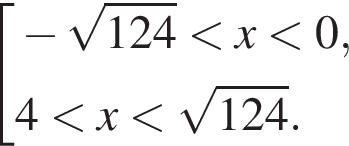
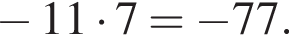
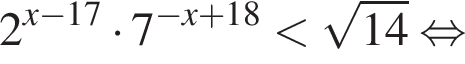
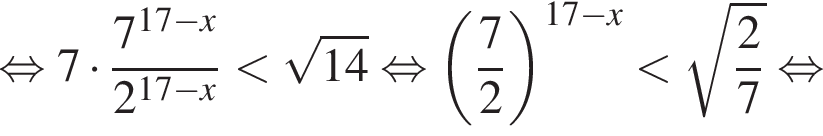
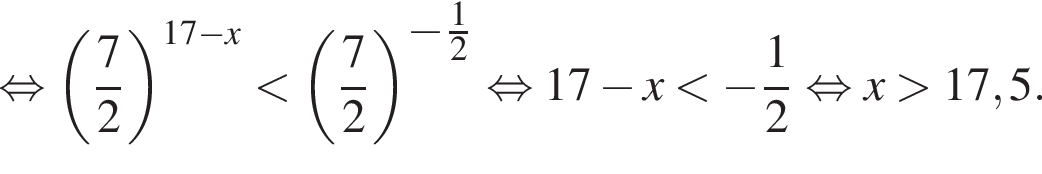
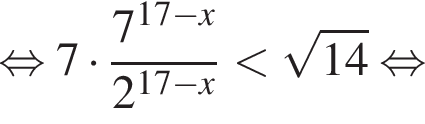
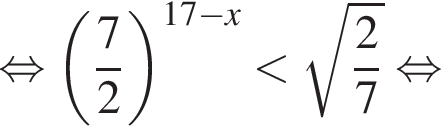

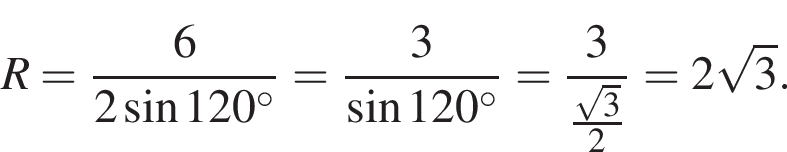
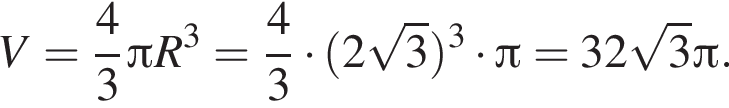
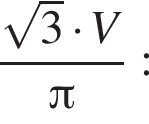
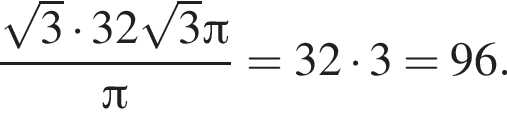
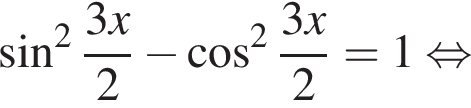
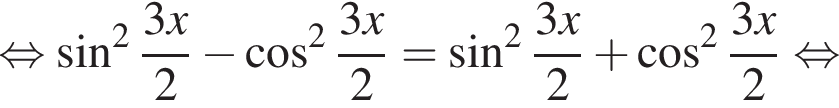
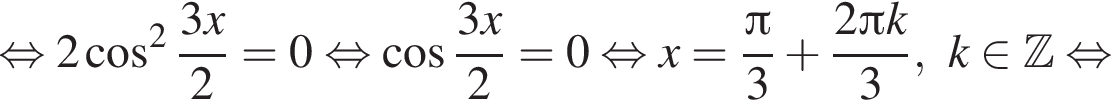
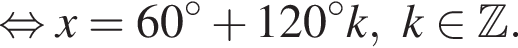
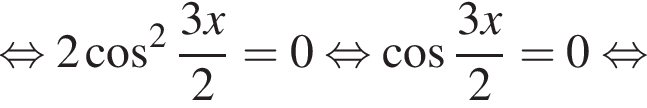
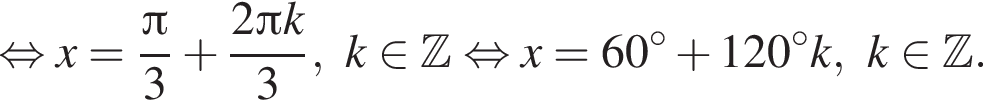
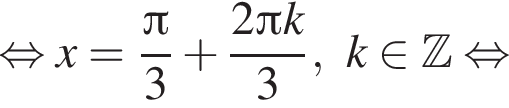
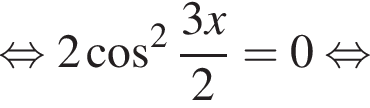
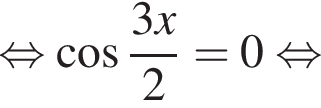
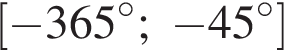 удовлетворяют решения x = −60°, x = −180°, x = −300°, сумма этих корней равна −540°.
удовлетворяют решения x = −60°, x = −180°, x = −300°, сумма этих корней равна −540°.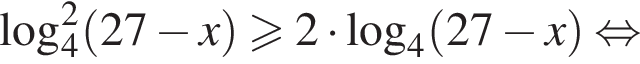
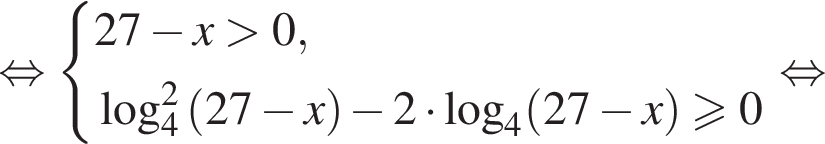
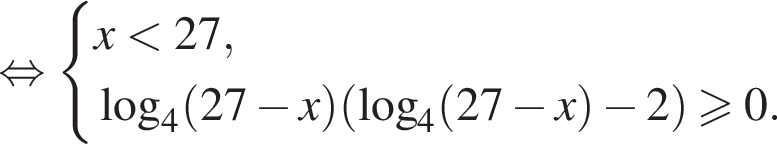

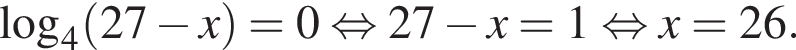
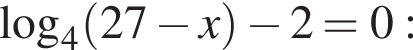

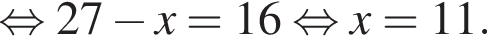
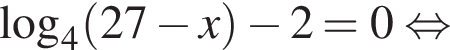
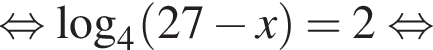
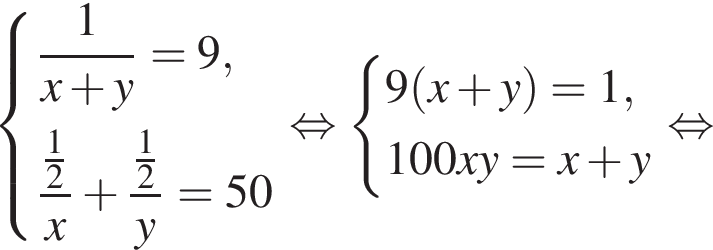
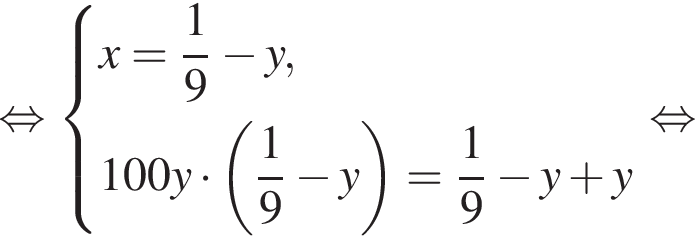
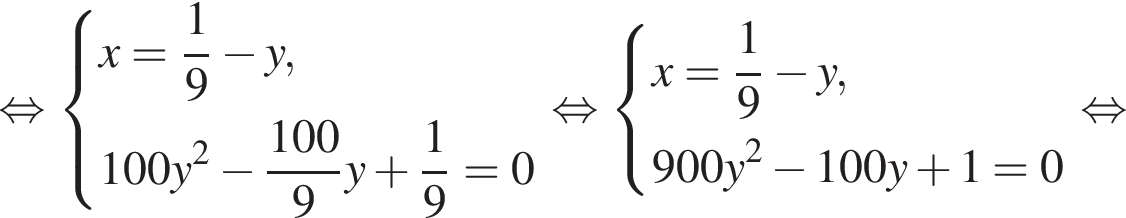
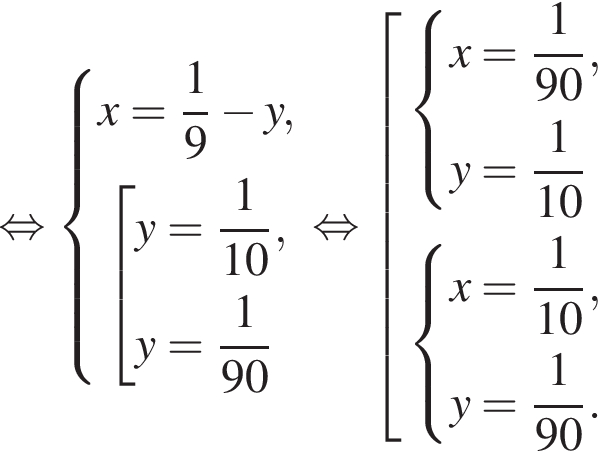
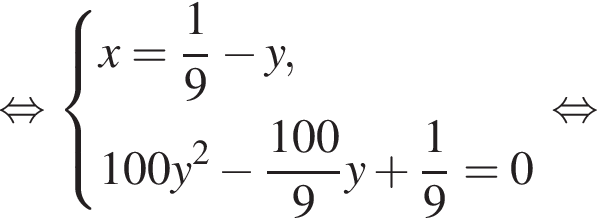
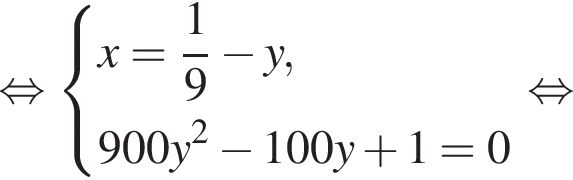
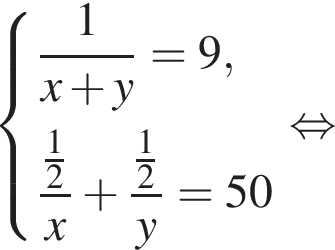
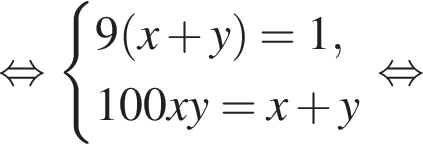
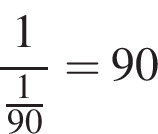 часов.
часов.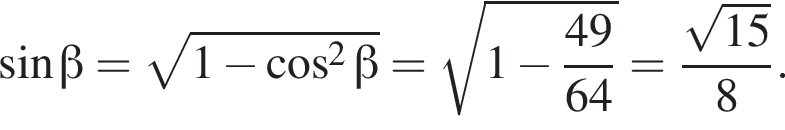
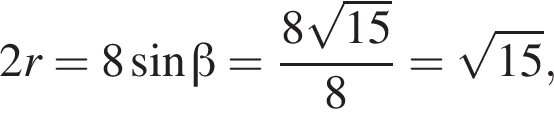
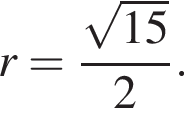 Тангенс угла α равен отношению высоты пирамиды к радиусу окружности, вписанной в ромб. Имеем:
Тангенс угла α равен отношению высоты пирамиды к радиусу окружности, вписанной в ромб. Имеем: